Table Of Content
In the columns to the right of the last factor, enter each response as seen in the figure below. The above table contains all the conditions required for a full factorial DOE. Minitab displays the standard order and randomized run order in columns C1 and C2, respectively. The first run (as specified by the random run order) should be performed at the low levels of A and C and the high levels of B and D.
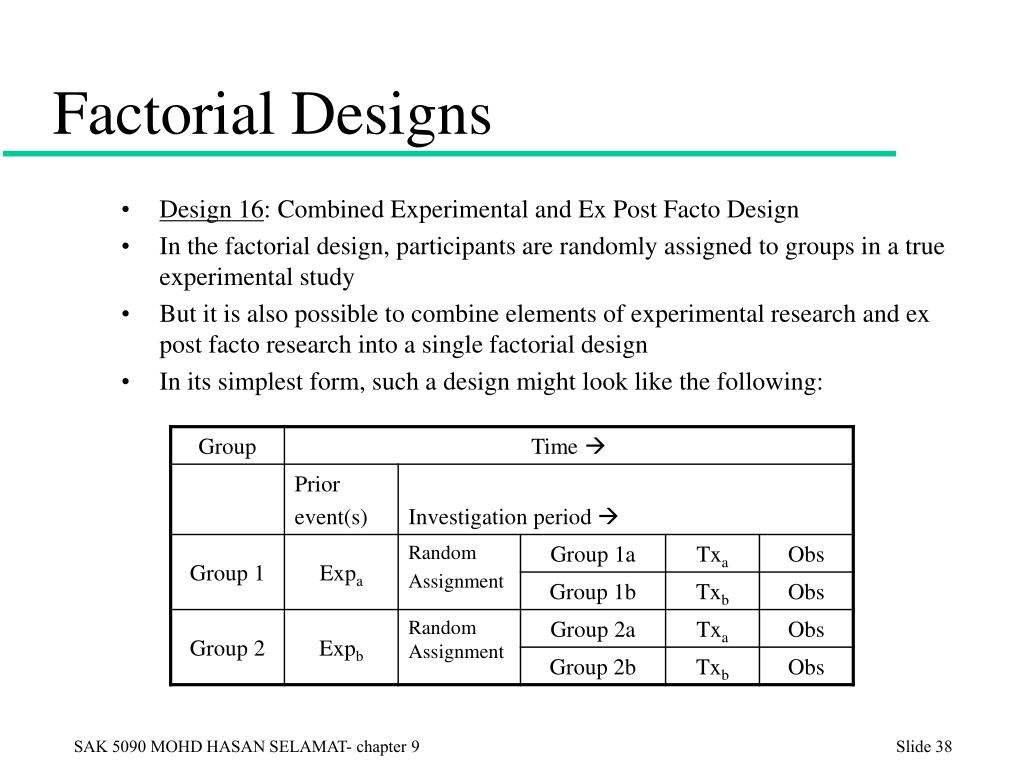
Assigning Participants to Conditions
However, let’s imagine that she is also interested in learning if sleep deprivation impacts the driving abilities of men and women differently. She has just added a second independent variable of interest (sex of the driver) into her study, which now makes it a factorial design. If these values represent "low" and "high" settings of a treatment, then it is natural to have 1 represent "high", whether using 0 and 1 or −1 and 1. This can be conducted with or without replication, depending on its intended purpose and available resources. It will provide the effects of the three independent variables on the dependent variable and possible interactions. Remember, an interaction occurs when the effect of one independent variable depends on the level of the other independent variable.
Implementing Clinical Research Using Factorial Designs: A Primer
This might seem surprising given that “correlation does not imply causation”. It is true that correlational research cannot unambiguously establish that one variable causes another. Complex correlational research, however, can often be used to rule out other plausible interpretations.
Normal Probability Plot for the Effects
One way to test this hypothesis is by categorizing salary into three levels (low, moderate, and high) and skills sets into two levels (entry level vs. experienced). Two-level factorial experiments, in which all combinations of multiple factor levels are used, efficiently estimate factor effects and detect interactions—desirable statistical qualities that can provide deep insight into a system. This gives them an edge over the widely used one-factor-at-a-time experimental approach, which is statistically inefficient and unable to detect interactions because it sequentially varies each factor individually while all the others are held constant. Factorial design can be categorized as an experimental methodology which goes beyond common single-variable experimentation.
This method can be used to capture detailed information about participants’ behavior or to analyze social interactions. Behavioral measures involve measuring participants’ behavior directly, such as through reaction time tasks or performance tests. These measures may be administered using specialized equipment or software.
Whether to Use an RCT or a Factorial Design
Social researchers often use factorial designs to assess the effects of educational methods, whilst taking into account the influence of socio-economic factors and background. An advantage of these graphs is that they display means in all four conditions of the design. Someone looking at this graph alone would have to guesstimate the main effects.
These experiments cannot really test whether or not the assumptions are being met - again this is another shortcoming, or the price of the efficiency of these experiment designs. Therefore all the two-way and three-way interaction effects are defined by these contrasts. Simultaneous examination of multiple factors at two levels can reveal which have an effect. From this one can see that there is an interaction effect since the lines cross.
Experiment Design Guidelines for Product Analysts — Part 2/3 - ResearchGate
Experiment Design Guidelines for Product Analysts — Part 2/3.
Posted: Mon, 12 Jul 2021 07:00:00 GMT [source]
Non-Experimental Studies With Factorial Designs
A factorial experimental design is an experimental design that is used to study two or more factors, each with multiple discrete possible values or “levels”. Factorial experiments can be used when there are more than two levels of each factor. However, the number of experimental runs required for three-level (or more) factorial designs will be considerably greater than for their two-level counterparts.
Factorial designs are therefore less attractive if a researcher wishes to consider more than two levels. A factorial experiment allows for estimation of experimental error in two ways. The experiment can be replicated, or the sparsity-of-effects principle can often be exploited. Replication is more common for small experiments and is a very reliable way of assessing experimental error. When the number of factors is large (typically more than about 5 factors, but this does vary by application), replication of the design can become operationally difficult.
The different ICs when used in real world settings would entail different amounts of contact or different delivery routes and their net real world effects would reflect these influences. Thus, it is important to recognize that such effects do not really constitute experimental artifacts, but rather presage the costs of complex treatments as used in real world application, presumably something worth knowing. For example, imagine that a researcher wants to do an experiment looking at whether sleep deprivation hurts reaction times during a driving test. If she were only to perform the experiment using these variables–the sleep deprivation being the independent variable and the performance on the driving test being the dependent variable–it would be an example of a simple experiment. Computerized measures involve using software or computer programs to collect data on participants’ behavior or responses.
To do this, we collapse, or average over the observations in the hat conditions. For example, looking only at the no shoes vs. shoes conditions we see the following averages for each subject. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail.
As these researchers expected, participants who were lower in SES tended to give away more of their points than participants who were higher in SES. This is consistent with the idea that being lower in SES causes people to be more generous. But there are also plausible third variables that could explain this relationship. It could be, for example, that people who are lower in SES tend to be more religious and that it is their greater religiosity that causes them to be more generous. Or it could be that people who are lower in SES tend to come from certain ethnic groups that emphasize generosity more than other ethnic groups. The researchers dealt with these potential third variables, however, by measuring them and including them in their statistical analyses.
When we find that independent variable did influence the dependent variable, then we say there was a main effect. When we find that the independent variable did not influence the dependent variable, then we say there was no main effect. The other type of hypothesis—which is a major advantage of the approach—involves the assessment of interaction effects. These are observed when the effect of a factor is dependent on the level of the other factors in the experimental model. We have first discussed factorial designs with replications, then factorial designs with one replication, now factorial designs with one observation per cell and no replications, which will lead us eventually to fractional factorial designs.
But the experimenters also know that many people like to have a cup of coffee (or two) in the morning to help them get going. For example, imagine that researchers want to test the effects of a memory-enhancing drug. Participants are given one of three different drug doses, and then asked to either complete a simple or complex memory task.

These ideas can be confusing if you think that the word “independent” refers to the relationship between independent variables. However, the term “independent variable” refers to the relationship between the manipulated variable and the measured variable. Remember, “independent variables” are manipulated independently from the measured variable. Specifically, the levels of any independent variable do not change because we take measurements. Instead, the experimenter changes the levels of the independent variable and then observes possible changes in the measures. It would seem almost wasteful to measure a single dependent variable.
In the end, you want to make sure that you choose levels in the region of that factor where you are actually interested and are somewhat aware of a functional relationship between the factor and the response. This is a matter of knowing something about the context for your experiment. Factorial designs are the basis for another important principle besides blocking - examining several factors simultaneously.

No comments:
Post a Comment